Многие программы автоматизированного проектирования (CAD) предоставляют функциональные возможности, которые вращают объекты, рисуемые в рабочей области. Приложения, которые включают в себя возможности вращения, используют функцию SetWorldTransform, чтобы установить соответствующее преобразование мирового пространства в страничное. Эта функция получает указатель на структуру XFORM, содержащую соответствующие значения. Члены eM11, eM12, eM21 и eM22 структуры XFORM определяют соответственно, косинус, синус, отрицательные синус и косинус угла вращения.
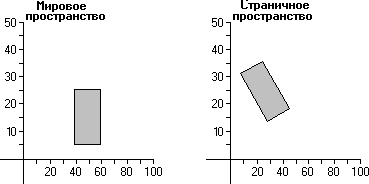
Когда происходит вращение (rotation), точки, которые составляют объект, вращаются относительно начала координат координатного пространства. На иллюстрации ниже показан прямоугольник 20 × 20 единиц, повернутый на 30 градусов при копировании из мирового координатного пространства в координатное пространство страницы.

На предшествующей иллюстрации, каждая точка в прямоугольнике вращалась на 30 градусов относительно начала координат координатного пространства.
Нижеследующий алгоритм вычисляет новую x-координату (x') для точки (x, y), которая повернулась на угол A относительно начала координат координатного пространства.
| x' = (x * cos A) - (y * sin A) |
Нижеследующий алгоритм вычисляет новую y-координату (y') для точки (x, y), которая повернулась на угол A относительно начала координат координатного пространства.
| y' = (x * sin A) + (y * cos A) |
Преобразования двух вращений могут быть объединены в матрицу 2×2, как показано ниже.
|
|x' y'| == |x y| * | cos A sin A|
|-sin A cos A| |
Матрица 2×2, которая произвела вращение, содержит нижеследующие значения.
|
| .8660 .5000| |-.5000 .8660| |
Образование Алгоритма вращения
Алгоритмы вращения основаны на тригонометрической теореме сложения, формулирующей, что тригонометрическая функция суммы двух углов (A1 и A2) может быть выражена в терминах тригонометрических функций этих двух углов.
|
sin(A1 + A2) = (sin A1 * cos A2) + (cos A1 * sin A2) |
Нижеследующая иллюстрация показывает точку p вращаемую против часовой стрелки в новую позицию p'. Кроме того, она показывает два треугольника, сформированные линией, нарисованной от начала координат координатного пространства до каждой точки и линии, нарисованной от каждой точки до оси X.
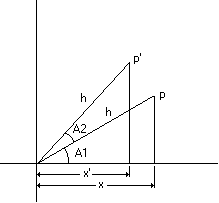
Используя тригонометрию, x-координата точки p может быть получена, путем умножения длины гипотенузы h на косинус угла A1.
|
x = h * cos A1 |
Y-координата точки p может быть получена, путем умножения длины гипотенузы h на синус угла A1.
| y = h * sin A1 |
Аналогично, x-координата точки p' может быть получена, путем умножения длины гипотенузы h на косинус (A1 + A2).
| x' = h * cos (A1 + A2) |
Наконец, y-координата точки p' может быть получена, путем умножения длины гипотенузы h на синус (A1 + A2).
| y' = h * sin (A1 + A2) |
Используя теорему сложения, предшествующие алгоритмы становятся нижеследующими:
|
x' = (h * cos A1 * cos A2) - (h * sin A1 * sin A2) y' = (h * cos A1 * sin A2) + (h * sin A1 * cos A2) |
Алгоритмы вращения для данной точки, вращаемой углом A2, могут быть получены, замещая x для каждого случая (h * cos A1) и замещая y для каждого случая (h * sin A1).
|
x' = (x * cos A2) - (y * sin A2) y' = (x * sin A2) + (y * cos A2) |